Enigmes Scolaires - Cours Thibaut

Cette série d’énigmes scolaires a pour thèmes majeurs les mathématiques et les sciences physiques. Les énigmes se veulent scolaires. Les énoncés feront donc appel aux connaissances acquises pendant la scolarité de l’élève. Ces énigmes à vocation ludique permettent néanmoins de tester le raisonnement et l’imagination de l’élève. Les énigmes ont 3 niveaux de difficulté:

Niveau (*) = niveau Collège
Niveau (**) = niveau Lycée
Niveau (***) = niveau Bachelier

Cherchez, questionnez Dr. Thibaut, interrogez-vous entre vous. Vous pouvez également consulter la rubrique « indices » pour vous aiguiller dans votre réflexion, puis en dernier recours regardez la solution de l’énigme dans la rubrique « solutions« .

Énigme du 25 août : « Marie et Marc ne discutent pas! » (*)

Marie met 30 minutes pour laver sa voiture, alors que Marc met 20 minutes. Combien mettent-ils à eux deux pour laver une voiture ?

Énigme du 26 août : « Une somme peut en cacher une autre! » (*)

Si nous additionnons, l’année de naissance de Thibaut, celle de son poisson rouge, l’âge de Thibaut au 31 décembre de l’année en cours et l’âge de son poisson rouge au 31 décembre de l’année en cours, qu’obtenons-nous ? Aurions-nous le même résultat en date du 1er janvier de l’année en cours ? Si, non, quel est ce résultat ?

Énigme du 27 août : « Pas d’athlète dopé mais du fractionné » (*)

Des jeunes athlètes ont participé à une compétition de 100 m. Quatre cinquième d’entre eux ont mis plus de 13 s. Parmi ceux qui sont passés sous les 13 s., deux septièmes sont descendus sous les 12 s. Combien d’athlètes ont couru entre 12 et 13 s ?

Énigme du 28 août : « Une Moyenne imbriquée » (***)

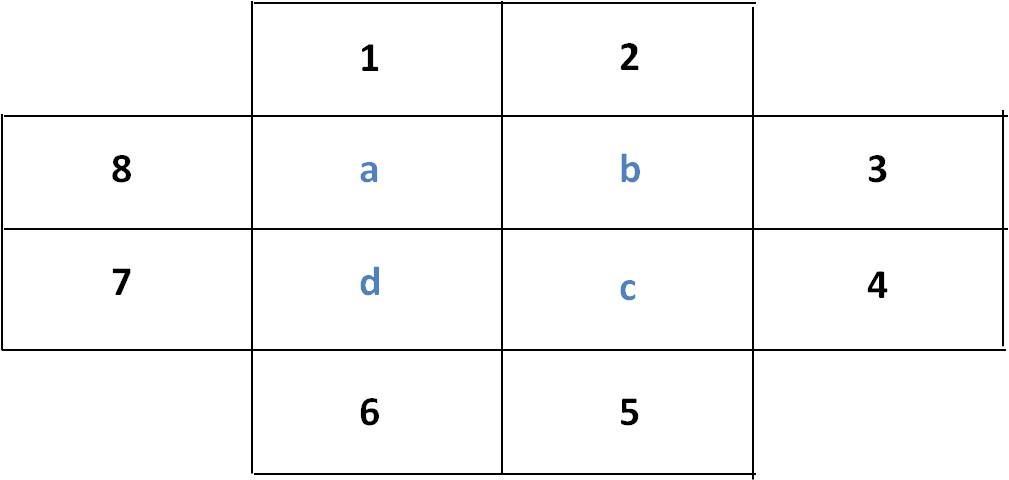
Il vous est demandé de retrouver les valeurs de a, b, c et d. La valeur de chaque lettre est la moyenne des 4 briques qui la juxtaposent.

Énigme du 31 août : « L’équerre change de profession! » (*)

L’équerre est un outil géométrique très utile en Mathématiques. Mais attention! Celle utilisée chez Cours Thibaut a des dimensions bien particulières: deux de ses côtés mesurent respectivement 30 cm et x cm (valeur inconnue) et le dernier le plus long mesure (10 + x) cm. Cet outil géométrique se transforme alors en outil mathématique. Quelle est la valeur de x ?

Énigme du 1er septembre : « Mieux vaut avoir les yeux dans le dos » (*)

Thibaut affiche une allure distinguée avec son chapeau. A tel point qu’à la rentrée, sa tenue vestimentaire devient virale et 5 de ses élèves portent désormais un chapeau. 3 chapeaux noirs et 2 blancs décorent les rangs de la classe. Il décide de tester la logique de ses élèves en plaçant en file indienne 3 d’entre eux. Tous orientés dans le même sens, le premier de la file ne pourra donc pas voir ses camarades de classe. Thibaut place 3 de ces chapeaux sur leur tête sans que les élèves connaissent la couleur de leur chapeau. En ouvrant les yeux seul le premier de la file explose de joie en clamant haut et fort: « Je connais la couleur de mon chapeau! ».

Énigme du 3 septembre : « Une inconnue remarquable » (**)

Nous vous donnons 3 égalités et la question est de déterminer la valeur inconnue x.

1. a + b + c = 1
2. 1/a + 1/b + 1/c = 0
3. a² + b² + c² = x

Énigme du 13 septembre : « Un second degré à débusquer » (** de Julia)

Sans utiliser de dérivation, déterminer la valeur pour laquelle la fonction f(x) = x + 1/x admet un minimum.

Énigme du 15 septembre : « Pesons les euros » (* d’Anaïs)

On dispose de 8 pièces de 1 euro dont une seule est fausse et plus lourde que les autres. Montrer qu’on peut la détecter en utilisant une balance de type Roberval en effectuant au plus deux pesées.

Énigme du 16 septembre : « Écriture sans double racine ! » (**)

Résolvez cette équation x² + (√6-√3)x -3√2 = 0 sans passer par des doubles racines.

Énigme du 21 septembre : « L’inconnue de trop! » (*)

De quoi rendre fou! Il est possible de résoudre une équation à une inconnue, ou un système de 2 équations à 2 inconnues, ou encore, un système à n équations et à n inconnues. Nous vous proposons de résoudre ce système à 3 inconnues mais avec seulement 2 équations (A, B et C sont des entiers positifs non nuls).

1. B + A + B x A = 34
2. C + A + C x A = 14

Énigme du 24 septembre : « Mieux vaut brûler le livre! » (***)

En additionnant le numéro de page de chacune des pages de son livre, un élève a obtenu une somme égale à 2014. En revanche, il a malencontreusement compté à 2 reprises une même page. A vous de retrouver ce numéro de page dédoublé et de déterminer le nombre de pages exact de ce livre.

Énigme du 25 septembre : « Sans poser de multiplication » (* de Laura)

Laura vous propose ce calcul à réaliser sans poser de multiplication (sans calculatrice). Soit f(x) = 43x – 42². Déterminez f(43).

Énigme du 26 septembre : « Le produit en cascade » (*)

Soit f(x) = (x-1/2).(x-1/3).(x-1/4)………(x-1/2013).(x-1/2014). Déterminez f(1).

Énigme du 28 septembre : « Qui n’aime pas le chocolat ? » (**) (Spéciale 1ES)

Lors d’un sondage de 160 personnes interrogées, 75% aiment le chocolat noir, 65% aiment le chocolat au lait et 45% aiment indifféremment les deux chocolats. Mais quel est le pourcentage de personnes qui n’aiment pas le chocolat.

Énigme du 29 septembre : « Air ball finalement précis ! » (***) (Spéciale 1S)

Un joueur de basketball peu adroit lance son ballon. Ce dernier quitte ses mains à une hauteur estimée de 2,10 m. Le ballon décrit une trajectoire parabolique et passe bien au dessus du panneau de basket. Le sommet de sa trajectoire est S (4 ; 3,78). Le repère étant défini par (Ox) l’axe lié au sol et l’axe (Oy) passant par la position du ballon à l’instant initial. A quelle distance de l’origine tombera le ballon ?

Énigme du 6 octobre : « Tu me prends vraiment pour un moulin à vent » (* d’Élisabeth)

Ce problème version « Mastermind » est un exercice récurrent dans la préparation au concours IFSI. L’exercice consiste ici à replacer dans le bon ordre les voyelles (pas de doublon ni de vide possible). Nous savons que sur chaque ligne 2 lettres sont bien placées, en revanche 2 autres lettres sont mal placées.

E Y A O I

A I O E Y

A I Y O E

A E I O Y

Énigme du 8 octobre : « Les Mathématiques et la Lecture » (*)

En Terminale S spécialité Maths on vous parle du triangle de Pascal et de son utilisation. Ici, nous vous proposons de compléter un autre type de triangle particulièrement curieux…

1211

111221

312211

Énigme du 13 octobre : « Et si la forme conjuguée ne suffisait pas ? » (***) (Spéciale TS)

Chercher la limite en -∞ de la fonction f(x) telle que f(x) = x + √(x²+4x+1).

Énigme du 19 octobre : « Pas cher la casserole » (***)

Les industriels recherchent à limiter le prix de revient de leurs produits. Expliquer pourquoi une casserole de 2l de volume possède un diamètre autour de 18cm.

Énigme du 6 novembre : « Combinaison gagnante » (* de Charline) (2nde pro)

Quelle est la probabilité de tirer 8 numéros gagnants parmi 9 numéros distincts ?

Énigme du 2 décembre : « Château limité » (** d’Héloïse) (Spéciale 1S)

Si je possède 6 jeux de 52 cartes et désire réaliser un unique château de cartes. Si j’utilise un maximum de cartes, quel niveau pourrai-je atteindre ?

Énigme du 9 décembre : « Comment comparer les croissances ? » (*** de Fleur)(Spéciale TS)

Déterminer la limite en 0 par valeur positive de la fonction suivante: f(x) = (x²+x+2)e^-1/x / x

Énigme du 15 décembre : « La balance se déséquilibre » (*)

Le poids d’une personne a diminué de 10% le premier mois, puis a augmenté de 10% le second mois. De combien son poids a varié au bout des deux mois ?

Énigme du 18 décembre : « Quand arrivera l’ascenseur » (**)

Un ascenseur va du rez-de-chaussée au 6^ième étage. Il met 6 s pour monter d’un étage, soit 7 m de haut, et s’arrête 16 s à l’étage demandé. Partant du rez-de-chaussée et s’arrêtant au 1^er, 3^ème, 4^ème et 6^ème étages, quelle est sa vitesse moyenne (unité km/h) entre le départ au rez-de-chaussée et l’arrivée au 6^ème ?

Énigme du 20 décembre : « Des cheveux dans les yeux » (*)

Lulu, Jea-Jea et Panpan sont 3 amis très différents physiquement (aux cheveux châtains-blonds, bruns et violets et aux yeux émeraude, aventurine et turquoise).

– Jea-Jea partage des chocolats suisses avec la personne aux yeux aventurine. – La personne aux yeux turquoise joue au badminton avec la personne aux cheveux bruns ainsi qu’avec Lin Dan. – La personne aux yeux émeraude a rencontré Lulu une fois. – Panpan, pro du laser quest, enseigne cette activité à la personne aux cheveux bruns. – La personne aux yeux aventurine mange des burgers avec Lulu. – La personne aux cheveux châtains-blonds aime jouer en ligne avec la personne aux yeux aventurine même si elle perd régulièrement.

Énigme du 24 décembre : « Un problème de taille » (** de Fantine) (Spéciale 1S)

Fin 2008 et après les fêtes de Noël, le jeune Santa a un tour de taille de 42 cm. Fin gourmet, il mange des chocolats toute l’année jusqu’au jour de Noël suivant, il augmente régulièrement de tour de taille de 6%, puis, perd systématiquement 1,2 cm de tour de taille lors de sa ronde épique de la nuit de Noël. Sachant que le diamètre de ma cheminée mesure 100 cm, en quelle année dois-je m’inquiéter pour mes cadeaux de Noël ?

Énigme du 20 janvier : « Le carré parfait » (* de Damien)

Un carré parfait est le carré d’un nombre entier. Montrer que quelque soit le nombre entier n, n²-6n+9 est toujours un carré parfait.

Énigme du 1^er février : « Tu me prends vraiment pour un moulin à vent ! » (*)

Trois moulins moulent trois sacs de farine en trois heures. Combien de sacs de farine neuf moulins moulent-ils en neuf heures ?

Énigme du 3 février : « Une collision s’impose ! » (*** de Marie Paula)

Un projectile P₁ est lancé verticalement depuis le sol selon l’axe (Oy) à la vitesse Vo=50ms^-1. Un second projectile P₂ est lancé une seconde plus tard dans les mêmes conditions. Tous deux sont soumis à une accélération a =-10j. A quelle altitude aura lieu la collision ?

Énigme du 12 février : « Des noms bien curieux » (**)

Quatre personnes font le bilan de leurs congés. A l’aide des indices ci-dessous, retrouvez le nom de famille, le lieu de congé et le mois de vacances de chaque personne.

Igor, dont le nom de famille n’est pas Teurdetex est partie en vacances à Deauville mais pas en juin.
Eddy, dont le nom de famille n’est pas Tounet, n’est pas partie en vacances ni en juillet, ni à la Baule.
La personne qui est partie en vacances à Nice en août ne s’appelle pas Teurdetex.
Mylène Micoton est partie en septembre mais elle n’est pas la personne qui est partie à Saint-Malo, laquelle ne s’appelle pas Sontrocteur. Aucune de ces deux dernières personnes ne se prénomme Patrice.

Énigme du 13 février : « Maudit pigeon! » (*** Spéciale Terminale S)

Un golfeur frappe une balle à une vitesse estimée à 100 m.s^-1 et avec un angle α entre le vecteur unitaire lié au sol et le vecteur vitesse initial. Sa trajectoire est telle qu’elle vient heurter un pigeon situé à une hauteur de 32 m et à une distance de 108 m par rapport au point d’origine. Quel est l’angle α correspondant à ce tire malencontreux ? (On prendra g = 9,81 m.s^-2)

Énigme du 15 février : « Un problème d’équivalence » (* de Solène)

Ce problème d’équivalence peut être posé lors d’un concours IFSI. Sachant que 2+55 est équivalent à 7 et 55+7 est équivalent à 222. En sommant chaque symbole 2, 5 et 7, lequel des 4 nombres suivants est le plus grand ? Vous l’aurez compris 2 ne correspond pas au chiffre 2 etc. Voici les 4 propositions: A) 77225722 B) 2577577 C) 77257225 D) 55777575

Énigme du 23 février : « 2 méthodes à comparer! » (*** Spéciale Terminale S)

Déterminer la limite en +∞ de ln(x+1)-x. Deux méthodes sont attendues comme réponse et seules les croissances comparées de type lnx/x et e^x/x sont autorisées !

Énigme du 12 mars : « La boucle est bouclée » (*)

Un avion transporte 500 briques. Il y en a une qui tombe. Combien en reste-t-il ?
Comment mettre un éléphant dans un frigo en 3 étapes ?
Comment mettre une girafe dans le frigo en 4 étapes ?
Le roi des animaux, le lion, fête son anniversaire. Tous les animaux sont présents à l’évènement sauf un, lequel ?
Est-ce que grand-mère peut traverser les marécages où vivent les crocodiles ?
Grand-mère est décédée en traversant les marécages, comment ?

Énigme du 15 mars : « Des satellites diophantiens » (*** de Lucie)

M. Bézout observe dans sa lunette astronomique un satellite qui apparaît périodiquement tous les 105 jours. 6 jours plus tard, il observe un autre satellite dont la période de révolution est de 81 jours. Combien de jours doit-il attendre pour les observer tous les 2 le même jour ?

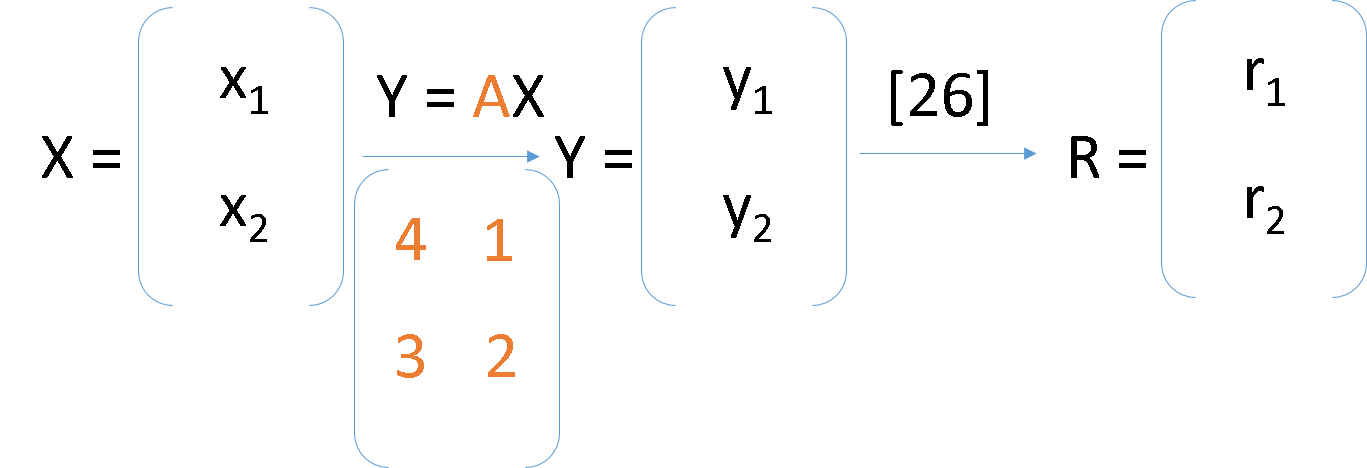
Énigme du 16 mars : « Message matriciel égaré ? » (***)

Un jour, je retrouve sur le pas de la salle un message farfelu: « WITQNOKLEDVU IWGVQW ? »
Malheureusement le moyen pour décoder ce message manque. Seule la manière de coder ce message a été laissée. Les lettres de l’alphabet sont rangées dans l’ordre et numérotées de 0 à 26. Le codage opère sur 2 lettres. Ainsi, 2 lettres à coder sont remplacées par une matrice colonne X (x1,x2), elle même est multipliée par une matrice carré A pour donner Y (y1,y2), enfin Y est transformée en la matrice R(r1,r2) qui est le reste de la division euclidienne par 26. Les entiers r1 et r2 donnent 2 lettres du message à coder. Je remarque également sur une partie pliée de la feuille que B = 5A^-1. Saurez-vous décoder ce message ?

Énigme du 25 mars : « Chute en parachute à vitesse contrôlée » (*** de Clara)

On considère un parachutiste en chute libre. La force de frottement liée à l’air dépendant de la vitesse de chute est -µV avec µ = 12,36 kgs^-1. La masse du système est 70 kg et g = 9,81 ms^-2. Quelle est la vitesse limite du chute du parachutiste exprimée en kmh^-1 ?

Énigme du 27 mars : « Changer de vitesse, mais quel rapport ? » (*** de Clara)

Un coureur A s’élance et court à une vitesse constante V_A = 10 ms^-1. 10 secondes plus tard, un coureur B s’élance à son tour et court à 20 ms^-1 pendant 20 m puis ralentit à la vitesse de 15 ms^-1. Au bout de combien de temps le coureur B rattrapera-t-il le coureur A ?

Énigme du 1^er avril : « To be or not to be » (*)

Les élèves de Terminale des lycées Louis Barthou et Saint-Dominique ont pris un tel retard dans la préparation des thématiques exigibles en Anglais pour l’épreuve d’oral du baccalauréat que l’académie a suspendu en ce jour cette épreuve. Bientôt, les lycées de Saint-Cricq et de Saint John Perse suivront également cette requête du ministère de l’éducation. Cependant, un problème de coefficient général de l’épreuve du baccalauréat s’impose. De combien sera donc augmenté le coefficient de l’épreuve écrite d’Anglais pour que la note maximale totale de toutes les épreuves ne soit pas changée ?

Énigme du 9 avril : « Angle de tir » (*** Spéciale Terminale S)

Déterminer l’angle de tire d’un canon (position d’origine assimilée au sol) pour que le rapport x_P/y_S=4 avec x_P l’abscisse de la portée du tire et y_S l’ordonnée du sommet de la trajectoire parabolique.

Énigme du 15 avril : « Singapore Maths Olympiad 2015 » (***)

Albert and Bernard just become friends with Cheryl, and they want to know when her birthday is. Cheryl gives them a list of 10 possible dates: May (15,16,19) , June (17,18) , July (14,16) , August (14,15,17).

Cheryl then tells Albert and Bernard separately the month and the day of her birthday respectively.

Albert: « I don’t know when Cheryl birthday is, but I know that Bernard does not know too. »
Bernard: « At first I don’t know when Cheryl’s birthday is, but I know now. »
Albert: « Then I also know when Cheryl’s birthday is. »

Enregistrer